0 前言

     五軸數控加工技術近年來被廣（guǎng）泛的應用於民用工業和軍事工業產品的加工。由（yóu）於同傳統三軸加工相比增加了兩個附加的自由度，五軸加（jiā）工能夠獲得更高的（de）生產效率（lǜ）和更好的加工質量，因此成為了數控領域（yù）研（yán）究的重點（diǎn）。

     五（wǔ）軸加工中的刀具路徑規劃問題一直是能否實現（xiàn）高效的自由曲麵加（jiā）工的關鍵。目前（qián），在實（shí）際生產中應用較多（duō）的刀具路徑規劃方法還是比較基本的等（děng）參數（shù）線加工方法和（hé）等截麵線加工方法[1]，由於上述方法（fǎ）均為按事先給定的方向確定加工路徑，加工表麵殘餘高度誤差的分布不均勻（yún），為保證最大殘餘高度誤（wù）差而使（shǐ）走（zǒu）刀行距過於保守，加工效（xiào）率偏低。因此提高加工效率，充分發揮五軸（zhóu）數控加工設備的性能是亟待解決的問題[2]。

    為了產生高效合理的刀具路徑，國內外學者提出了多種不（bú）同的方法，並且在應用中取得了一定的成效。國外學者如RAO 等（děng）提出Principal axis 方法， PI 等提出Grind-free 方法，LIN 等發展出誤差（chà）自適應生成算法；周豔紅、周雲飛、高軍（jun1）和楊勇生等國內學者也在這個方麵進行了深入和細致的研（yán）究，提出了不同的五軸刀具軌跡生（shēng）成算法並（bìng）得到了實際應用（yòng）。大部分現有的方法（fǎ）采用類似的（de）處理過程（chéng），從曲麵的一條邊界作為初始（shǐ）路（lù）徑，通過一定的算法得（dé）到偏置的（de）後續路徑。本文采用了一種新的方法，通過計算曲麵各處的有效加工域的寬度和最優（yōu）域加工方向，搜索得到曲麵（miàn）上一條優化的初（chū）始化路徑，並且構建了一種迭代算法生成相鄰的刀具路徑。最終生成的(近似)最優路徑具有最大的切削寬度和最短的刀具路（lù）徑總長度。

1 有效加工域參數計算

     數控加工成形過程就是刀具沿著預（yù）定的刀具路徑對工件毛坯進行切削（xuē）加工，最（zuì）終形成工件外形的過程。切削過程中刀具通過掃掠在被加工表麵形成了一個加工區（qū）域，此加工的部分區域與理想加工麵的誤差小於或（huò）等於預定的加工（gōng）精度要求，而其餘部分區域則不符合加工精度要求。本文將符合加工精度要求的那部分加工區域定義為有效加工域。可見，要將工件（jiàn）表麵加工成形，必須（xū）滿足有（yǒu）效加工域完全覆蓋被（bèi）加工麵這一要（yào）求。

     有效加工域的兩個最（zuì）重要的特征參數是域寬度和域（yù）切削方向。域寬度表征有效加工域覆蓋區域的大（dà）小，域切削（xuē）方向表征了產生（shēng）的刀具路徑的（de）流向，直接（jiē）影（yǐng）響域寬（kuān）度值。兩者都會（huì）對最終產生的刀具路（lù）徑質量產生重大的影響，因此（cǐ）是本文描述的重（chóng）點。有效加工域參數計算的（de）目標就（jiù）是得到具有（yǒu）最大域寬度的刀具路徑及其流向。有效加工（gōng）域的形成涉及到加工（gōng）表麵與加工刀具的相互作用，對（duì）其研究必然牽涉到對被（bèi）加工表麵的幾何特征和刀（dāo）具（jù）的幾何特征的描（miáo）述問題。對於工件被加工麵的描述已經有了統一的數學表達，因此主要討論刀具的幾何描述（shù）問題。

     1.1 刀具（jù）的統一參數表達

    為了使得分析過（guò）程不局（jú）限於（yú）某種特殊形狀的刀具，需要尋求一種刀具的（de）通用表達形式，使其可以用於各種加工刀具。由於NC 加工中刀具的旋（xuán）轉速度相對進給速度來說（shuō）要快的多，所（suǒ）以可以用一係列相連的（de）直線或（huò）曲線（xiàn）的回轉麵（miàn）來表示刀具的幾何（hé）形狀，所以本文采用了如圖（tú）1 所示的通用（yòng）刀具統一參 數表達[3]。

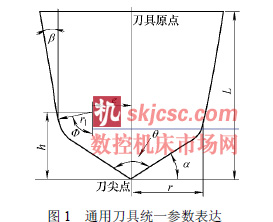
     部（bù）分、中間的圓環部分和（hé）下麵的圓錐部分。其（qí）中參數r 表示刀具的名義半徑，h 表（biǎo）示倒角圓的圓心到刀尖的垂直距離（lí），L 表示刀具的軸向長度，e 表示倒（dǎo）角圓的圓心到刀軸的徑向距離。其他的（de）四個角（jiǎo）度參數α，β，θ，φ分別如圖1 標示。改變各變（biàn）量的取值（zhí）便（biàn）可以得到各常用刀具模型。如圓環銑刀可以表示為（wéi）一種α =β = 0，e = r – r1 的（de）通用刀具。由（yóu）刀具的（de）統一參數表達可以建立了刀具的幾何（hé）描（miáo）述矩陣（zhèn）Mt [3]，本文不再贅述。

     1.2 有效（xiào）加工域寬度（dù）和域切削方（fāng）向

    有效加工域寬度是影響（xiǎng）生成的刀（dāo）具路徑質量（liàng）最重要的因素。其值大（dà）小與（yǔ）刀具在工件表麵切削時的姿態有關。為方便描述刀（dāo）具在加工麵上的運動姿態，在刀具與工（gōng）件表麵的接觸點A 處引入一個局部坐標係(Oxl yl zl )，如圖2 所示。

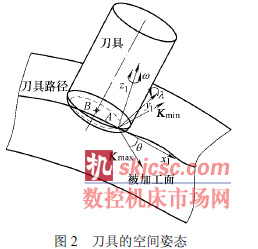
      圖 2 中點B 為刀（dāo）具中心（xīn）位置點，xl 軸的方向為A 處（chù）的瞬時切削方向，zl 軸的方（fāng）向為A 的曲麵外法線方向，yl 軸的方向由xl 軸和zl 軸通過（guò）右手螺旋法則確定。λ定義（yì）為刀具繞yl 軸的（de）傾角，ω 定義（yì）為刀具繞（rào）zl 軸的擺轉角[4]。kmax 表示被加工麵A 處最大主曲率方向單位矢量，kmin 表示A 處的最（zuì）小主曲率方向單位矢量。

     在加工中，每個時刻刀具掃描體外形與被（bèi）加工麵（miàn）的相互作用生成了此刻的（de）刀具有效掃描體外形，從而最終（zhōng）決定了切（qiē）削產（chǎn）生的幾何形貌。瞬時的（de）刀具（jù）有效掃描體（tǐ）外形上的任意一點P 必須滿足條（tiáo）件：P點處刀具掃描體外形（xíng）曲麵外法線矢量必須與的此時的（de）刀具運動向量相垂直。當刀具有效掃（sǎo）描體外形確定後，通過計算刀具（jù）有效掃描體外形上的點（diǎn）與工（gōng）件表麵的距離（lí），就可以確定有效加工域的寬度b。設刀具有（yǒu）效掃描（miáo）體（tǐ）外形上的存（cún）在兩個位置點P1、P2，這兩點與被加工（gōng）曲麵的距離等於預定的加（jiā）工公差要求τ，則有效加工域寬度的定義（yì）如下

     即有效加工域寬度可以表示如下：刀具有效掃描體外形上與（yǔ）被加工曲麵的距離等於τ的兩點（diǎn），此兩（liǎng）者之間的（de）距離（lí）在垂直於切削方向(矢（shǐ）量Yl方向)上的投影長度（dù）。

     為了得到最大的域寬度值，加工時應當讓刀具調（diào）整姿態在無幹涉的條件下盡可能的匹配被加工表麵的幾何形（xíng）貌。因此域寬b 是一個關於刀具幾何描述Mlt (s)和公差τ的函數。同時還應注意到，在（zài）曲麵的某處（chù），不同的切削方向得到的有效加（jiā）工域寬（kuān）度是（shì）不同的。如圖3 所示，在被加工（gōng）曲麵的某處P，刀（dāo）具沿著θa 方向切削時相對應的有效（xiào）域寬度為ba，沿著θb 方向切削時對應的（de）有效域寬度為（wéi）bb，此時兩者刀具的空間姿態Mlt (s)和預定的公差τ都相同，但得到的有效域寬度不同。

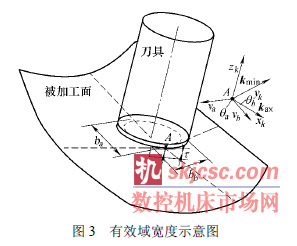
     現在引入一（yī）個（gè）新的局部坐標（biāo）係( Ox y z κ κ κ ) ，xκ軸（zhóu）的（de）方向為A處的曲麵最大主曲率方向( max κ 方向（xiàng）)， yκ 軸的方（fāng）向為曲麵最（zuì）小（xiǎo）主（zhǔ）曲率方向( min κ 方向)，zκ軸的（de）方向為P 點處的（de）外法線方向。定義瞬時切（qiē）削方向和xκ 軸的夾角為切削方向角θ。綜（zōng）上所述，b 也（yě）是關於切削方向角θ的函數。即b =W(Mlt (s), θ , τ ) =W(Mt (s), λ , ω, θ , τ ) (4)通常，當切（qiē）削方（fāng）向與最（zuì）小主曲率方向相同或非常接近時，可以取到最（zuì）大的有效域（yù）寬度（dù）[5-6]。

    為減少計算量（liàng），本方法以一定間隔（gé）均勻分布（bù）的曲麵參數（shù）u，v 采樣該處的優化有效域寬度和切削（xuē）方向角，得到一個離散的優化域寬度和切削方向角的曲麵分布。對於未采樣（yàng）的曲麵區域，可以通過相鄰的四個采樣（yàng）點的數值插（chā）值計算出未采樣點（diǎn）的域寬度和方（fāng）向角數值。從這個意思上說，有效加工域規劃方法是一種近似最優的刀具路徑（jìng）生成算法。

2 刀具路徑的搜索迭代生成（chéng）

     傳統的刀（dāo）具路徑生成算法一般都從曲麵（miàn）的某一條邊界開始計算生成刀具路徑。這種方法雖然方便了計算過程，但不能保證由此（cǐ）邊界產生的刀具路徑即是最優的。有效加工域規劃法采用搜索算法得到整個曲麵（miàn）上一條最優（yōu）的初（chū）始（shǐ）刀具路徑，通常情況下這條初始路徑不是曲麵的邊界；然後通過迭代算法生成其餘的偏置路徑，最終使得生成的路（lù）徑（jìng）完全覆蓋整個曲（qǔ）麵。

     2.1 最優初始路徑的搜（sōu）索確定

    通過上麵所（suǒ）述的方法我們得到了被加工曲麵上均勻分布的有效加工域，以及每個加工域的域寬度和（hé）切削方向角的集合。成為初始刀具路徑的（de）要求是此路（lù）徑通過的（de）有效加工域應該具有最大的平（píng）均有效域寬度。搜索曲麵四個邊界上的有效加工域，參考每個有（yǒu）效加工域的切削方向角確定下一個有效加工域，連接這兩個有效加（jiā）工域作為刀具路徑的一部分，重（chóng）複此過程直到（dào）遇到處於曲麵（miàn）邊界上的有效加工域停止。這樣便（biàn）生成了一係列的（de）刀具路徑，因為每（měi）條路徑都是沿（yán）著各個離散加工（gōng）域（yù）的最佳切（qiē）削方向生成的，因此這些路徑上的每一個有效加工域都取到了（le）本域的最大域寬度（dù）。這些路徑稱為候選初始路徑。然後從這一係列候（hòu）選初始路徑中選（xuǎn）出具有最大平均域寬度的一條路徑做為（wéi）初始路（lù）徑。設有（yǒu）N 個離散的有效加工（gōng）域位於某段候選初始路（lù）徑上，此路徑的（de）平均域寬（kuān）度bav 定義為

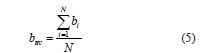
     式中bi —— 編號 i 的路徑的最大域寬度值計算出每條候選路徑的平均域寬度值 bav，取bav 最大值的路徑作為（wéi）初始路（lù）徑。

     2.2 後（hòu）續刀具路徑的迭代生成

     確定了最佳初始路徑後，便可以通過迭代算法生成（chéng）相鄰的路徑。迭代算法通過一條（tiáo）已知的（de）刀（dāo）具路徑生成相鄰的一條路徑，然後利用剛生成的路徑重複算法過程產生（shēng）下一條路徑，如此往複循環直到所有（yǒu）的有效加工域都被路徑覆蓋。下麵具體介紹迭代算法的具體實現。

     引入一（yī）個新的（de）參數 f，f 表（biǎo）示當前路徑的（de）實際平（píng）均域寬度（dù）與（yǔ）初始路徑的（de）平均域（yù）寬度bav_max 的比值，稱為刀具路徑的質量係數，即

     式(7)說明要取的路徑TPi+1 上的對應點（diǎn）Pi+1, j 與當前Pi, j 的連線方向與有效域寬度的方向（xiàng）相同，即在yl軸方向上。設加工曲麵的參數表達為S(u,v)，計算保證最大域寬度條件下的（de）Pi+1, j 坐（zuò）標必須滿足

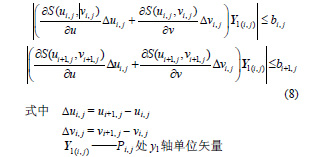
     在實際加工時，刀具的空間姿態和被加工曲麵的（de）幾何特性在每（měi）個不同的（de）A 處都不同，因此具有不同的有效加工域寬度和（hé）切削方向角。這意味著兩（liǎng）條相鄰的刀具路徑通常不會（huì）是相互平行的[7]。為了防止生成的相鄰的（de）刀具路徑間存在沒有被刀具路徑覆蓋的間隙，還需（xū）對刀具路徑進（jìn）行校驗和調整（zhěng），使之滿足下麵兩個要求。
 

     (1) 相鄰兩條刀具（jù）路徑的邊（biān）界線沒有交點。

     (2) 相鄰兩（liǎng）條刀具（jù）路（lù）徑至少在曲麵某一處（chù）重合。

     條件(1)保證了兩條相鄰（lín）路徑的邊（biān）界或者是每處都互相有一（yī）部分重疊，或者是沒有任何一（yī）處重疊。條件(2)保證了兩條相鄰路徑必定有一處重合（hé），即排除了條件一中完全不重疊的情況。這就保證了相鄰的刀具路徑都相互重疊一部（bù）分（fèn），路徑間不存在間隙。通過上述方法，以路徑TPi 為基礎（chǔ）生成路徑TPi+1，然後以路徑TPi+1 為基礎生成（chéng）路徑（jìng）TPi+2，整個（gè）刀具路徑生成的過程就是上述方法的迭代過程。

     隨著迭代（dài）過程的進行，通常情況下所生成刀具路徑（jìng）的質量係數將逐漸減小，為了保證得到高效的刀具路徑，必須對產生的刀具（jù）路徑的質量係數進行一定的限製，否（fǒu）則迭代的後期可能（néng）產生大（dà）量的質量不佳的刀具路徑。本（běn）文采取的方（fāng）法是預先設定質量係數的下限fmin，當檢測到當前生成的刀具路徑的質量（liàng）係數低於fmin 時，則停止本次迭（dié）代（dài）過程。然後在未加工區域中重複上述的搜索（suǒ）迭代算法，得到新的初始路徑，以初（chū）始（shǐ）路徑為基礎進行新的一輪迭代運算。如此（cǐ）往複，直到被加工表麵上的所有有效加工域都（dōu）被刀（dāo）具路徑覆蓋時結束算法運行。

3 算法的實現及應用示（shì）例

     3.1 算法實現流（liú）程

     在微機上以上述算（suàn）法為基礎，采用Matlab 和Visual C++環境編寫（xiě）程序實現算法過程。算法程序流程如圖4 所示。

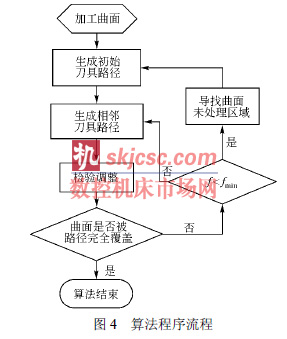
     程序以已知（zhī）的被加（jiā）工曲麵作為輸入，以最終的優化刀具路徑集作為輸出，並且可以根據用戶需要改變刀具路徑質量係數的下限值以及有效加工域在曲麵上的分布密度。

     3.2 應用示例（lì）

     選取熱壓塑模具曲麵的一部分作為示（shì）例被（bèi）加（jiā）工麵，在（zài）xyz'a'c 型的五軸數控機床環（huán）境下采用環形刀（dāo）具進行切削加（jiā）工（gōng）。刀具的名義半徑r = 8 mm，圓環（huán）角圓半徑r1 =1.5 mm。刀具的兩個錐度角α = β = 0o，加工預定公差τ= 0.05 mm。為了方便比較，將刀具傾角λ和ω 設置為固定值，λ= 10o，ω=3o，刀具路徑最小質量係數設為fmin = 0.75。

采用（yòng）傳統的等參（cān）數（shù）線法（fǎ）和（hé）本文提出（chū）的有效加工域規（guī）劃（huá）法分（fèn）別（bié）生成相應的刀具路徑，下表是兩種方法的結果對比。

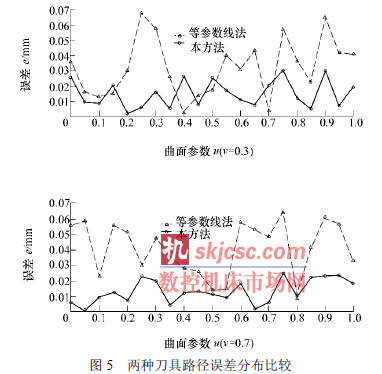
     采用上述兩種方法生成的刀具路徑（jìng）在VERICUT 下進行曲麵誤（wù）差分布模型數據分析，圖5顯示了（le）兩種刀具路徑誤差分布比較。

     上述對比結果可以看出，有效加工域規劃方法（fǎ）生（shēng）成的刀具路徑數目和總（zǒng）長度（dù）都減少了，尤其（qí）是路（lù）徑（jìng）總（zǒng）長度減（jiǎn）少了35.5%，與等參數（shù）線法相比較，采用（yòng）有效加（jiā）工域規劃法可以得到更短的刀具路徑總長度以及加工質量更高的加工表麵。不（bú）足的是快速移動路（lù）徑的長度反而加大了，作者認為這是由（yóu）於等參數（shù）線法采（cǎi）用之字型走刀方式，因此刀具快速移動的距離比較短，而有效加工域規（guī）劃法沒（méi）有對路徑的進退刀（dāo）點進（jìn）行優化，這（zhè）一不足（zú）也是今後對本方法進一步完善的重（chóng）要方向（xiàng）。

4 結（jié）論

     (1) 提出了一種新的五軸數控加工刀具路徑生成方法——有效加工域規劃法。這種方法根據刀具的幾何特征（zhēng）和空間姿態結合曲麵的幾何特性，構造曲麵上的有效（xiào）加工域集合，計（jì）算得到(近似)最優的域寬度和切削方向（xiàng）角參數。同時構造了一種搜索迭代算法，用於得到初始路徑和相鄰的後續路（lù）徑。

     (2) 應用（yòng）示例顯（xiǎn）示有效加工域規劃（huá）法相對（duì）於傳統的五軸（zhóu）刀具路徑生成算法具有較明顯的優勢，同樣的加工條件下可（kě）以得到總長度更短的刀具路徑和更短的加工時間，並（bìng）且能得到更高的加工精（jīng）度。

     (3) 應用過程中也（yě）發現了本方法的一些不足，如刀具路徑質量係數的選擇依靠主觀判斷（duàn），不參與切削的刀具路徑(如快速（sù）移（yí）動路徑)沒有得到足夠的優化等，需要進一步的改進完善（shàn）。