基於SYNTEC的螺旋錐齒輪加工機床數（shù）控係統（tǒng）開發（上）
2017-1-3 來源：沈陽工業大學 作者：張西棟（dòng）
摘要
SYNTEC-10B 數控係統是台灣新代科技股份有限公司研發的一款具有較高（gāo）性價比的產（chǎn）品，該數控係統具有很好的開放性，是數控係統二次開發的良好平台。弧（hú）齒錐齒輪數控加工涉及到的參（cān）數較多，齒輪規格調整後需要重新編製加（jiā）工程序，而且數控編程不直觀，人機交互性差。為了解（jiě）決不同弧齒錐齒輪加工的數控編程的繁瑣性問題，提高加工效率，利用 e HMI 軟件對 SYNTEC-10B 數控係統的人機交互界麵進行了客製，使其能夠通過（guò）屏幕界麵（miàn）直接輸入弧齒錐齒輪（lún）的基本參數的形式，即可生成相（xiàng）應的數控加工程序，完成自動化加工。
對螺旋錐齒輪的齧合原理以及加（jiā）工過程進行了分析，對相對微分法、齧合方程的確定、等距共軛原理以及第二共軛曲麵的確（què）定等內（nèi）容進行了描述。分析了螺旋錐齒輪的加工原理和方法、局部（bù）共（gòng）軛原理及齒麵（miàn）數學模型的建立，為後（hòu）續界麵的開發提供了理論基礎。
利用 e HMI 軟件對弧齒錐齒輪加工過程中參數輸入、模擬仿真（zhēn）等相關界麵進行（háng）了客製與設計（jì）。搭建了客製（zhì）化（huà）界麵係統（tǒng）的整體框架圖以及弧齒錐齒輪加工係統的（de）人機界麵的工作流程圖。通（tōng）過建立專案，添加相關畫麵檔與（yǔ）功能鍵的形式對整個人機界麵進行了（le）客製。設計製作了齒製（zhì）選（xuǎn）擇、加工參數輸（shū）入、刀（dāo）具參數輸入等主要畫麵檔，將齒輪加工所需要的各種參數信息通過不同（tóng）組件的形式添加（jiā）在畫（huà）麵檔上，使相關的參數輸入界麵簡潔明了，便於（yú）機床操作者進行相關（guān）的數控編程。
為了配合畫麵檔的切換、參數輸入等動作（zuò），相應地（dì）客製設計了與各級畫麵檔相對應的功能（néng）鍵。通過測（cè）試仿真模塊，對開發的（de）多窗（chuāng）體界麵中的各級畫（huà）麵檔與功能鍵相（xiàng）關客製工作進行了仿真檢測，確保了各種參數（shù）的正確性。通過整個分析設計過程，最終達到參數的輸入、加工代碼的生成、加工仿真程序的運（yùn）行整個過程的人（rén）性化和快（kuài）速化。
構建了人機界麵的各層級關係框圖，使界麵之間的層級關係一目了然；按照操（cāo）作習慣對（duì）數控係統軸群顯示界麵進行了設置。基於客製的要求，通過（guò）搭建架構圖（tú）的形式對客製過（guò）程中的新代數控係統內裝型 PLC 進行了總結。將 R 寄存器（qì）中允許操作者讀寫的（de）地址分配給客製（zhì）過程中的各輸入變量，最後將客製的專案進行了（le）軟件封裝。
關鍵詞：新代數控係統，螺旋錐齒輪，畫麵檔，測試仿真
第（dì） 1 章 緒論（lùn）
1.1 課題來源及（jí）研究背景
1.1.1 課題來源
基於課題組的科研項目《大型螺旋錐齒輪專用數控機床的（de）開發》，提出了本課題。該科研（yán）項目是沈陽市科技創新專項資（zī）金（jīn）—工業科技攻關專項（F15040200）支持的項目。項目中的數控機床（chuáng）采（cǎi）用的是台灣新代（dài）科技有限公司開（kāi）發的，具有較高性價比的SYNTEC-10B 數控係統；該係統（tǒng）操作簡（jiǎn）單，開（kāi）放性較好，能夠滿足弧齒螺旋錐齒輪加工的基本要（yào）求。為了提（tí）高數控係統的人機交互性，適應不同生產批次的零部（bù）件加工要求，滿足數（shù）控機床普通操（cāo）作者的（de）操作要（yào）求，對 SYNTEC 數（shù）控係統人機界麵進行專用化地客製。
1.1.2 課題研究背景
計算機作為 20 世紀人（rén）類最偉大的科技發明，推動了整個社（shè）會的變革。計算機技術以及相關（guān）的控製技術在機械製造領域中（zhōng）的應用促使製造行業生產形態（tài）發生了（le）重大轉變。1952 年美國（guó）推出了（le）世界上第 1 台數控銑（xǐ）床，至今（jīn）已經（jīng）過了 60 多個年頭，在這段時間裏，車床、磨床、銑床、衝壓床、電加工機床（chuáng）、鏜床、加工中心以及各類專用機床慢慢發（fā）展起（qǐ）來，逐漸形成一個完備的數控機床家族體（tǐ）係。數控係統（tǒng）經過半個多世紀的發展，先（xiān）後（hòu）經曆了硬件數控和軟件數（shù）控兩個發展階段[1] 。
1952 年發展起來的電子管類數控係統開啟了硬件數控係統階段，該類數控係（xì）統是這一階段的第 1 代。由於硬件的限製，早期計算機運行速度較低，不能滿足數控加工實時控製的要求，為此，技術人員將數字邏輯電路嵌入到一台專用計算機中，組成數控裝（zhuāng）置，這種數控裝置即為硬件連接數控，簡稱數控（NC）。 1961 年以晶體管分離（lí）組件為基礎發展起來的數控係統（tǒng）取（qǔ）代了以笨重的電子（zǐ）管為組（zǔ）件搭建的數控係統，這使得數控係統（tǒng）的體積得到縮小，促使其（qí）在工業生成中的廣泛應用，這就是第 2 代數控係統。 1965 年發展（zhǎn）起來一種（zhǒng）功耗低（dī），體積更小的集成電路（lù）構成的 NC 係統，該型 NC
係統的可靠性更高，數控係統進（jìn）入第 3 代。
軟件數控階段是以（yǐ） 1970 年小型計算機的應用為標誌。同時，數（shù）控（kòng）係統的發（fā）展進（jìn）入到第 4 代，軟件慢慢取代硬件來完成更多的功能，“軟連（lián）接”數控時代開始（shǐ）引（yǐn）領數控加工的行業（yè）發展（zhǎn）。
1974 年（nián）采用微處理器芯片的 CNC 係統開始投入使用，數控係統進入（rù）了以微機為背景的時代，同時數控係統進入到第 5 代階段。微處理器型的 CNC 係統實現了機電一體化，這大大降低了製造成本，縮小（xiǎo）數控係統的體積，提高了數控係統的普及程度。
1990 年發展起來的基於個人 PC 機（jī）的數控係統是（shì）第 6 代（PC-Based）。這一（yī）代是以大（dà）容量存（cún）儲器、大規模集成電路、CRT 應用為（wéi）標誌（zhì）。第 6代數控係統具備更完善的控製功能，具有（yǒu）實時精（jīng）度補償、三維圖形顯示校驗、交互式編程等（děng）軟件技術。同時這一代數控係統具有（yǒu）了模塊化（huà）、柔性化、係列化、標準化的雛（chú）形。
第 6 代數控係統已經具有了明（míng）顯的優點。利用（yòng） PC 平台的優勢，數控係（xì）統的技術進（jìn）步以及（jí）更新升級都比較快捷。第 6 代數控係統具有較高的元器件集成度，可靠性高，性能更加（jiā）優越，而且第 6 代數控係統提供了開放式的開發平台，這更有利於軟硬件資源優勢的發揮（huī），拓寬了數（shù）控係統的（de）應（yīng）用領域。
1958 年由（yóu）北京機床研究所和（hé）清華大學研製的第一代（dài）電子（zǐ）管 101 數控機床標誌著我國數控機床進入第（dì）一代階段，開啟了我國數控係統研製的（de）曆史序幕[2]，我國數控係統發展曆史如表 1.1 所示。
表 1.1 數控係統（tǒng）發展（zhǎn）曆史
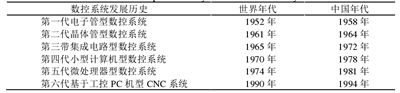
數控技術是一種將機械製（zhì）造技術、成組技術（shù）、現代控製技術、計算機技術、網絡通訊技術、光機電技術、微電子技術、傳感檢測技術、信息處理（lǐ）技術、液壓（yā）氣動技術集（jí）合（hé）在一起的係（xì）統（tǒng）技術，是現代製造（zào）技術的基礎[3]。數控係統在數控技術中（zhōng）處於核心的地（dì）位，其（qí）性（xìng）能（néng）的強弱直接影響數控設備加工效能的高低，而且（qiě）對整個製造（zào）係統的升級發（fā）展、高效運轉、自動化（huà）控製具有重要作用[4]。計算機技術的飛速發展，推動著數控係統向開放式、標準化方向發展，出現了一（yī）些（xiē）不同層次的開放式數控係統[5]。新代科技（jì）股份有限公司順應時代發展，推出（chū）了開放式的 SYNTEC 數（shù）控係統（tǒng），其開放式的數控係統設計方便用戶進行（háng）係統功（gōng）能的二次開發。 數控是數字化控製（Numerical Control, NC）的簡稱。數控是指利用數字化信息實行的控製，即利用數字控製技術實現的（de）自動控製係（xì）統[6]，這是數控（kòng）的廣義含（hán）義。從狹義（yì）上來說就是利用數字化信息對（duì）機床軌跡（jì）和狀態進行控製，例如（rú）數控車床、數控（kòng）衝床、數（shù）控銑（xǐ）床、數控加工中心等[7]。數控係統嵌入到機床本體中就組成（chéng）了更具較高附加值的技（jì）術密集型產品-數控機床，它可以實現加工過程的自動（dòng）化控製[8]
在實際的數控生產中，經常會遇到同一係列不同尺寸規格的零件，這需要每一個規格的零部件單獨編製一個數控加工程（chéng）序，編製程序的工（gōng）作量就會很大，十分煩瑣不便[9]。在西門子數（shù）控係統中，雖然自身帶有某（mǒu）些（xiē）固定循環功能可供機（jī）床操作者使用，但是（shì）它的界麵不直觀（guān），不友（yǒu）好，且對應用場（chǎng）合的限製較多[10]；而在發那（nà）科係（xì）統中，雖然可通過二（èr）次開（kāi）放 G 功能的方式實現固定循環，但是其（qí）界麵也不（bú）夠直觀，不完善，對操作者（zhě）的技術要求較（jiào）高[11]。
1.2 弧齒（chǐ）錐齒輪加工現狀
1.2.1 國外研究現狀
英國人 Hum Phris 在 1970 年最早提出了圓弧齒形的設計思路[12]，以這個思路為基礎，慢慢發展到了後（hòu）來的弧齒錐齒（chǐ）輪。該型齒輪的齒麵計（jì）算公式（shì）是非線性方程組，所以齒麵形狀較為（wéi）複（fù）雜[13]，加工要求比（bǐ）較高。螺旋錐齒輪具有重合度（dù）大、傳動平穩、承載能力高等直齒錐（zhuī）齒輪不具備（bèi）的性能優點，因而（ér）這促使了該型齒輪在相交和（hé）交錯軸傳動場合（hé）中的廣泛應用。基於該型（xíng）齒輪優越的性能，對螺旋錐齒輪進行相關研（yán）究的重要性在世界範圍內得到廣泛的認同。而美國
Gleason 公司的 E.威爾德哈泊以（yǐ）及 M. L.巴斯特爾初步提出了（le）弧齒錐齒輪理論[14]，以（yǐ）此為基礎，Gleason 公司通（tōng）過對弧齒錐（zhuī）齒輪的深入研究，形成了特（tè）有的弧齒錐齒輪相關技術，奠定了（le）其在世界上的壟斷地位。圖 1.1是弧齒錐齒輪齧合傳動示意圖。
圖 1.1 弧齒錐齒輪齧合傳動示意圖
曲齒錐齒輪分（fèn）為延伸外擺線（Oerlikon 和 klingelnberg）和準雙（shuāng）曲麵（Gleason）兩種齒製[15]，曲齒錐齒輪的加工製造技術要求比較高，目前世界上隻有三家（jiā）公司具有（yǒu）相關的技術，分別是美國 Gleason（格裏森）、瑞士 Oerlikon（奧利康）和德國 Klingelnberg（克林根貝爾格）[16]。準雙（shuāng）曲麵齒（chǐ）輪在軸線相交時即為弧齒錐齒輪，其應用最廣泛，這種齒輪采（cǎi）用（yòng）間歇分齒法銑（xǐ）齒加工而成，調整加工的過程複（fù）雜。
國內外學者對曲齒錐齒輪進行了深入的研（yán）究。60 年代初 Gleason 公（gōng）司的 Baxter 和Wildhaber 通過對局部（bù）共軛齒麵副的齒麵接觸過程分析，提（tí）出了準雙曲麵錐齒（chǐ）輪節麵數學模型理論（lùn），這（zhè）提高了Gleason 公（gōng）司（sī）弧齒錐齒輪理論的成熟度[17,18]。由於格（gé）裏森公司在弧齒（chǐ）錐齒輪技術上的進步，以局部共軛原理（lǐ）作為弧齒（chǐ）錐（zhuī）齒輪設計和加工的基礎，形成了一係列格裏森製（zhì）錐齒輪的設（shè）計和加工方法，鞏固了其在（zài）弧齒錐（zhuī）齒輪加工領域的（de）壟斷地位。由於弧齒錐齒輪的加工過程是一個反複調整機床參數（shù），反複試切的過程，加工效率（lǜ）比較低， Baxter 提出了弧齒錐齒輪（lún）的齒（chǐ）麵接觸分析（Tooth Contact Analysis，簡稱 TCA）方法。這種方法是基於計算機平台運行的，以加工機床的調整參數為依（yī）據，建立齧合（hé）齒輪的齒麵數學方程，利用數學理論研（yán）究齒輪在不同安裝形式下的齒麵接觸情（qíng）況和（hé）傳動誤差，通過（guò）研究齒麵接觸區，對機床調整參數進行修正。美國的著名教授 Litvin 提出“局部綜合法”[19-24]的切齒加工方（fāng）法，首先給出決定齒輪齧合區寬度（dù）和位置、接觸軌跡方向等傳動質量的相關（guān）條件，然（rán）後利用微分幾何的數學理論，推算小輪齒麵在參（cān）考點處的主方向（xiàng）和主曲率，進而（ér）得（dé）到小輪加工的機床調整參數。Litvin 教（jiāo）授提出的預置（zhì）拋物線型誤差傳遞函數是這種方法的基礎[25]，由於安裝誤差所造成的線性傳遞誤差可以通（tōng）過這種（zhǒng）方法自動吸收掉，這（zhè）對於（yú）齒輪傳動中振動、衝擊以及（jí）噪聲（shēng）的（de）降低是有利的。
（1）Gleason 公（gōng）司錐齒（chǐ）輪加工係統準雙曲麵錐齒輪加工機床是（shì）美國 Gleason 公司的主要經營產品，是格裏森公司具有（yǒu）自主知識產（chǎn）權的機床，但是它采（cǎi）用的是齒輪傳動機構，其機械傳（chuán）動機構比較複雜[26]，由傳動鏈（liàn）較長引起的製造誤差比（bǐ）較（jiào）明（míng）顯。二十世紀八十年代（dài），格裏森公司以鳳凰係（xì）列螺旋錐齒輪加工機床為標誌，掀起了該類機床的重大改革創新（xīn）。這種機床（chuáng）是一種五軸聯（lián）動的多功能機（jī）床，可加工多種齒製的螺（luó）旋錐齒輪，除了需要手動（dòng）更換（huàn）夾具、刀盤、工件以外，其餘的加工過（guò）程均是自（zì）動化完（wán）成的，相對機床來說，加工精度能夠高出 1-2級，而且重複精（jīng）度較好。格裏森公司與德國 Zeiss 公司合作開發了誤差分析和三座標測量係統，將（jiāng）這個係（xì）統連接到鳳凰係列機床上，構成（chéng）誤差閉環係統：G-AGE。該係統在（zài）準雙曲麵加工中可以通過一（yī）次試切的方式獲得滿意（yì）的齧合配對。
在 CIMT-99 展（zhǎn）會上，SRS405 型數控剃齒刀磨床和 450G 型數控（kòng）螺旋錐齒輪磨齒機被格裏森公司以鳳凰係列主力機（jī）型的形式推出了。450G 型磨齒機可以按照 3-4 級精度精磨齧合的硬齒麵螺旋錐齒輪小輪和大輪，其加工工件（jiàn）的最大模數為 12mm，最大加工（gōng）直徑達到了 450mm，聯軸節齒麵或（huò）者弧齒（chǐ）鼠牙（yá）盤也囊括在（zài）其加工（gōng）範圍之內，表現出（chū）了優異的加工性（xìng）能。450G 型數控機（jī）床可（kě）以實現包括砂輪修整運動在內的八軸（zhóu）聯動，它用其中的五軸聯動實現了錐齒輪加工（gōng）中的磨齒運動[27]。目（mù）前格裏森公司生產的較為成熟的（de）數控磨齒機（jī）有 200G、450G、800G 以及（jí）銑齒機 Phoenix116CNC、175HC、275HC、450HC、100HC 等係列產（chǎn）品（pǐn）。
（2） Oerlikon 公司錐齒輪加工係統 瑞士（shì） Oerlikon（奧立康）公司在 CIMT-99 展會上展出（chū）了一台可實（shí）現幹切削的型號為 C28 的六（liù）軸五聯動的數控螺旋錐齒輪銑齒機[27]。為了排屑的方便，該型機床將刀（dāo）盤主軸箱的滑鞍安裝在了傾斜床身的導軌上。我國湖北省某車橋有（yǒu）限公司曾於 1997 年（nián）引（yǐn）進了 Oerlikon 公司的 C28 型銑齒機，該車橋公司成為中國第一家（jiā）采用該型數控銑齒機的用（yòng）戶。隨著生（shēng）成的發展，這種環保型數控銑（xǐ）齒機以其優異的加工性能（néng）受到各企業（yè）的青睞，慢慢發展成為汽車後橋主從動螺旋（xuán）錐齒輪加工的關鍵設備。
（3）Klingelnberg 公司錐齒輪加工係統（tǒng） Klingelnberg（克林根（gēn）貝（bèi）爾格）公司開發出一種型號為 KNC/S35 的萬能數控（kòng）弧（hú）齒錐齒輪切齒（chǐ）機床，該型機床把齒輪測量技術內嵌到機床（chuáng）中，精簡了機床機構，改善了機床的剛性；提高了機械的響應速度，保證了 NC 指令的可靠性，齒輪加工的精度得到提高。將計算機技術應用於齒輪加工機床可以提（tí）高加工精度，降低生產成本，增大負載能力和降低噪聲（shēng）。Klingelnberg 公司采用新（xīn）的計算機技術之後推出 HPG、HPG-S 兩種型號的錐齒（chǐ）輪加工機床。
1.2.2 國內研（yán）究現狀
為了打破格裏森公司在弧齒錐齒輪加工領域的技術壁壘，前蘇聯（lián）和日本等國的科學家對格裏森製齒輪進行了（le）研究和學習，相關的研究學習雖然推動了弧（hú）齒錐齒輪理論的發展，但（dàn）是始終沒有（yǒu）突破弧齒錐齒輪的齧合理論問題。我國的（de）相關技術人員從 70 年代開始對弧齒錐齒輪齧合理論的數學基礎進行了係統的研究。為了推進該技術的研究進展，我國原機械工業部（bù）於 1972 年將“格裏（lǐ）森成套技術的研究”列為重（chóng）點攻關的科研項目，同（tóng）時得到了許多知名學（xué）者、高等院校的支持（chí）。我國科研人員（yuán）通過不懈的努力，在弧齒錐齒（chǐ）輪齧合理論方麵取得了重大進展[28]。龔道香教授等相關學者（zhě）通過（guò）研究計算，得到了螺（luó）旋錐齒輪的齒形精密測量以及相應的誤差處理方法[29]，為了求得實際齒（chǐ）麵和理論齒麵之間的偏差函數，先用誤差補償的方（fāng）法求得（dé）齒形誤差，再用該齒形誤差作為全齒麵比較法的初始值來求解。鄭昌啟教授利用嚴謹的數學解析法對共軛齒輪齧合理論中的基本原理進行了研究（jiū）[30,31]，以此為依據，推算揭示了 Gleason 螺旋錐齒輪（lún）的機床調整、齒坯設計、刀具參（cān）數的計算和（hé）輪齒檢驗原理（lǐ）以及方法。曾（céng）韜教授提出了節麵分析法[32]，利用該（gāi）方法對準雙曲麵齒輪的節點曲率和節點參數進行計算，將相關的計（jì）算結果推送給螺旋錐齒輪的（de）切（qiē）齒計算（suàn）和輪坯設計（jì），推算出格裏森調整計算卡的相關公（gōng）式。
李左章、王延（yán）忠等教授學者采用三次 B 樣條函數（shù）的數（shù）學理論對齒麵采樣數據（jù）點進行數值擬合[33]，由此得到齒麵的擬合函數（shù），歸納出了基於齒麵離散數值點的接觸分析理論。蘇智劍教授利用齒麵接觸跡線、齒麵 NURBS、傳動比（bǐ）函數（shù）等已知（zhī）條件對準雙曲麵齒輪齒（chǐ）麵（miàn）的數學模型（xíng）進行了描述[34,35]，豐富了螺旋錐齒輪的設（shè）計計算方法和理論。
1.3 課（kè）題研（yán）究的目（mù）的與意（yì）義（yì）
以我單（dān）位引進的新代 SYNTEC 數控係統為平台，針對弧齒錐齒輪的（de）數控加工過（guò）程，對其進行（háng）二次開發，通（tōng）過編程（chéng），將現（xiàn）有的先進控製思想應用到數控係統中，完善其控製算（suàn）法，優化數控加（jiā）工的參數輸入界（jiè）麵、模擬仿真界麵，使其能夠通過屏幕界麵直（zhí）接輸（shū）入弧齒錐齒輪的一些基本（běn）參數，生成相（xiàng）應的數控加工程序，然後進行自動化加工。 數控係統（tǒng）是衡（héng）量一個國家製造業發展水平的重要指標，在製（zhì）造業中處於核心的位置。作（zuò）為我國國民經濟的（de）核心以及工業（yè）化的原動力，製（zhì）造業的總（zǒng）產值大約占全國國民生產總值的百分之四十左（zuǒ）右（yòu）。雖然製造業是（shì）我國國民經濟的支柱產（chǎn）業，但是數控（kòng）技術的發展水平（píng）較（jiào）國外發達國家相比差距較大，這限製了我國製造業的發展[36]。
裝備製造業在世界範圍（wéi）內蓬勃（bó）發展（zhǎn），信息技術在裝備製（zhì）造業相關技術產品的升（shēng）級換代中表現出的積極作用越來越（yuè）得到大家的重視與認可。數控技術與控製技術、計算（suàn）機技術、應用軟件相結合，推動了（le）數控係統的開發，樹立了傳統製造業信息化改造的典範。而先進控（kòng）製技術的主要任務（wù）是使數控（kòng）機床具有最大化的加工速度、加工（gōng）速度平滑性以及較小的加工誤差，通過與先進的製（zhì）造技術結合，縮小了國內與國外在（zài）硬件技（jì）術和軟件技術上的（de）差距（jù），這對於完善我單位項目中引進的新代 SYNTEC 數控（kòng）係統的功能，總結數控係統開發（fā）過程中的（de）經驗，提升國產數控係統性能和品質具有重要意義（yì）。
研（yán）究采用計算機仿（fǎng）真、優化的虛擬加工技術，實現了從加工編程到加工（gōng）仿真的全程虛擬化，可以有效的縮短產品生產周期（qī），減小生產成本。基於新代 SYNTEC-10B 數控係統平台的弧齒螺旋錐齒輪加工機床人機界麵設計，能夠提高錐齒（chǐ）輪加工的人（rén）機交互性，提高齒輪的加（jiā）工效率。新代數（shù）控係統人機界麵的客製能夠（gòu）適應螺旋錐齒輪係列化生產中由（yóu）於生產批次與型號的變（biàn）更，對數控（kòng）編程提出的便捷性要（yào）求。因此，本課題的研究（jiū）內容對（duì）加快產品研發，縮短製（zhì）造（zào）周期，促（cù）進螺（luó）旋錐齒（chǐ）輪（lún）的應用範（fàn）圍以及整個機械行業的（de）發（fā）展（zhǎn）都有著很高（gāo）的現實意（yì）義。
1.4 課題研究內容
台灣新代（dài）科技股份有限公司順應行業發展的需（xū）要，推出了便（biàn）於用戶二次開發的SYNTEC 係列的數控係統，它是一個良好的開放式平台，通過二次開（kāi）發可把客戶需要的（de）各功（gōng）能模塊集成到係統中，這樣既可以將操作者（zhě）工作經驗的（de）優勢發揮出來，又可以簡化工作流程，提（tí）高係（xì）統的（de）可維護性。 本課題以新代（dài） SYNTEC 數控係統為開發平台，以螺旋錐齒輪加工機床為研究對象，針對弧齒錐齒輪的加工進行了數控係統的（de）二次開（kāi）發。通過 e HMI 軟件對螺旋錐齒輪加工過程中參數輸入、模擬仿真等相關（guān）界麵進行設計與客製。設計開發（fā）的界（jiè）麵係統主要包括齒（chǐ）輪參數輸入、刀具參數設置以及加工參數設置等內容，客製的人（rén）機界（jiè）麵簡潔友好（hǎo），便（biàn）於操作。通過（guò）整個分析設（shè）計過程（chéng），最終（zhōng）達到界麵參數的輸入、加工代碼的生成、加工仿真程序（xù）運行整個過程的（de）虛擬化和快（kuài）速化，初步總結數控（kòng）加工中參數的優化和加工仿真過程的一般方法。圖 1.2 是 e HMI 的軟件工作界麵（miàn），圖 1.3 是螺旋（xuán）錐齒輪加工機床樣機，圖 1.4 是弧齒錐齒輪數控銑齒機示意圖。
圖 1.2 e HMI 工作界（jiè）麵
圖 1.3 螺旋錐齒（chǐ）輪加工機床樣機
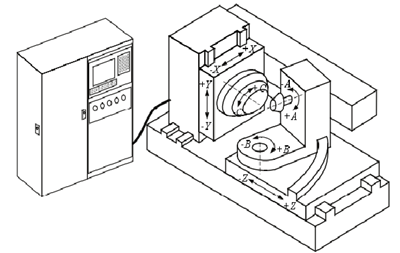
圖 1.4 弧（hú）齒（chǐ）錐齒輪數控銑齒（chǐ）機示意圖
1.5 本章小結
本章對（duì）課題來（lái）源及背景進行了闡述，通過對 Gleason 公司錐齒輪加工係統、Oerlikon公司錐齒輪加工係統以（yǐ）及 Klingelnberg 公（gōng）司錐齒輪加（jiā）工係統的分析，引出了對項目中的新代數控係統進行客製化改造的必要（yào）性，提出了課題研究的（de）目的（de）意義以及課題研究的主（zhǔ）要內（nèi）容。
第 2 章 弧齒錐齒輪加工原理
弧齒錐齒輪的數控加工過程涉及到的參數（shù）比較多，各（gè）參數之間的關聯性比較大，導致相關計算過程比（bǐ）較繁瑣；為了配合 SYNTEC-10B 數控係（xì）統（tǒng）的人機界麵開發的項目需要，對弧（hú）齒（chǐ）錐齒輪的齧合加工原理作簡（jiǎn）單分析。
2.1 弧齒錐（zhuī）齒輪齧合原理
弧齒（chǐ）錐（zhuī）齒輪齧（niè）合原理以（yǐ）齧合中運動曲麵接觸傳動關係為主要研究內容，如圖 2.1所示。局（jú）部共軛理（lǐ）論以及相對微分法是研究（jiū）齧合原理的主要方（fāng）法理（lǐ）論，首先以齧合方程為起點，然後通過相對微分的數（shù）學理論，以節點為計算參考點，確定完全共軛時瞬時齧合（hé）點處的撓率和曲率，最後（hòu）推算計算參考點處的曲麵參數（shù）[14]。
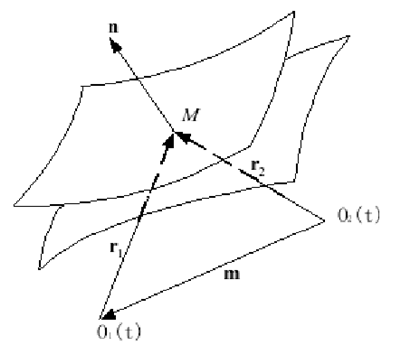
圖 2.1 運動曲麵的接觸傳動
2.1.1 相對微分法
通過上述分析得知：相對微分法能夠兼顧運動中（zhōng）曲麵的幾何問題以及運動問題，是研究（jiū）齒輪齧合問題的有效工具。
2.1.2 齧合方程
式（shì）子中的第（dì）一個方程是接觸條件方程，第二個方程是相（xiàng）切條件方程（chéng）。這是齒輪傳動的基本方程式。
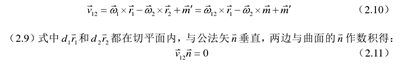
式（2.11）即為齧合方程，它表示兩運動曲麵持續齧合的前提條件是兩曲麵在法線方向的分速度必須相等。
如果兩運動曲麵在任何時刻（kè）都沿（yán）著齧合（hé）方程所確定的曲線接觸，則稱它們為線接觸共軛曲麵，即完（wán）全共扼曲（qǔ）麵；如果兩運動曲（qǔ）麵在任何時刻的接觸狀態是在線上，則稱它們為（wéi）點接觸共軛曲麵，即不完全共軛曲麵[37]。這兩種齧合形式（shì）在齧合位置處都滿足齧合的基本方程（2.8）和（2.11）。
2.1.3 確定第二共軛曲（qǔ）麵
在齒輪齧（niè）合原理中經常會遇（yù）到求解（jiě）某（mǒu）一（yī）共軛曲麵的問題，即根據一對共扼曲麵中的第（dì）一共軛曲麵s1和兩個曲麵之間的相對運動關係，求解第二共軛曲麵s2 。如果（guǒ）兩個曲麵能夠正常齧合，那麽曲麵S 2必定是齧合方程所確定的接觸線在運動坐標係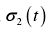 
中的軌跡，所以曲麵S2滿足方（fāng）程組（zǔ）[37]：
中的軌跡，所以曲麵S2滿足方（fāng）程組（zǔ）[37]：
2.1.4 等距共（gòng）軛（è）曲麵原理
（1）等距（jù）曲麵
設有兩個曲麵 S 和Sh，若對曲麵 S 上任（rèn）意一點 M，在曲麵S h上都能找到一點 Mh和它相對（duì）應（yīng），曲麵（miàn） S 上M點的法矢和曲麵nS 上（shàng） Mh點的（de）法矢都與MMh平行，而且MMh=h是一個常數，那麽（me）曲麵（miàn）S h稱為曲麵 S 的等距曲麵[37]。如圖 2.2 所示，若曲麵 S 的方程為 r ，單位法矢為 n ，則曲麵Sh 的方程可以表示為：
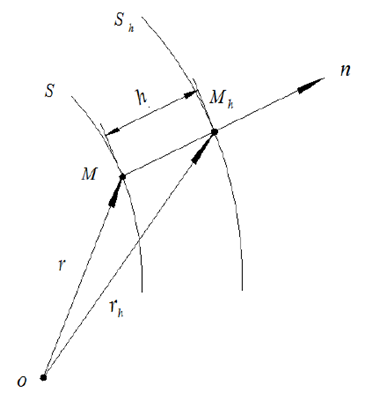
圖 2.2 等距曲麵樣圖
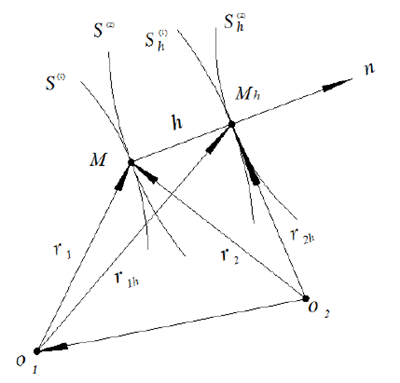
圖 2.3 等距共軛曲麵樣（yàng）圖
2.2 弧齒錐齒輪加工分析
2.2.1 弧（hú）齒錐（zhuī）齒輪加工原理和方法
項目中的（de）弧齒錐齒輪加工采用的是平（píng）頂產形輪原（yuán）理，其中大輪是右旋，它在加工時（shí）采用的是雙麵銑刀（dāo）盤（pán）；小輪是左旋，它在加工時采用的則是單麵銑刀盤。
弧（hú）齒錐（zhuī）齒（chǐ）輪與準雙曲麵（miàn）齒輪的加工都是在準雙曲麵銑齒機上完成的。該型（xíng）機床的設計加工原理如圖 2.4 所示，機床的搖台機構模擬齒輪，而安裝在搖台上的刀盤的切削麵則是模擬齒輪（lún）的（de）一個輪齒（chǐ）。當被加工齒輪輪坯與刀盤按照規定的傳動比繞（rào）各自的軸線旋轉（zhuǎn）時，刀盤（pán）就會在輪坯上切出一個齒槽。整個切削（xuē）過程就像（xiàng）一對準雙曲麵齒輪的齧合過程一（yī）樣，刀盤的切削麵與輪坯的輪齒曲麵（miàn）是一對完全共軛的齒麵，稱這種加工方（fāng）法為展成法[37]。
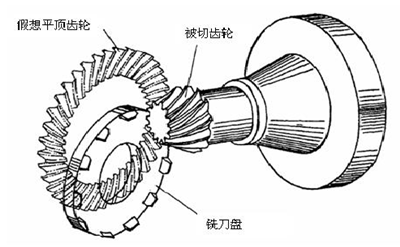
圖 2.4 螺旋錐齒輪加工原理圖
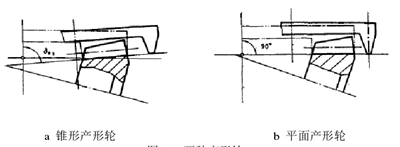
圖 2.5 兩種產形輪
為了能夠在弧齒錐齒輪（lún）的齒麵展成加工中完成齒根（gēn）曲麵的加工，應（yīng）該（gāi）保證工件的根（gēn）錐與刀（dāo）盤的刀尖平麵相切。圖 2.6 是大（dà）小輪齧合時的刀盤位置圖，通過圖 2.6 可以發現刀盤軸線不平行，這決（jué）定（dìng）了實際加工時既不能像用展成法加工大輪（lún）一樣將小輪加工用的刀（dāo）盤切削（xuē）麵做得和（hé）小輪切（qiē）削（xuē）麵一（yī）樣，也不能使大輪刀盤切削麵和小輪刀盤切削麵相互吻合，而用間接展成法完成加工。所以弧齒錐齒輪不能通過間接展成法和直接展成法完成加（jiā）工，需要局部共軛原理來加工[37]。
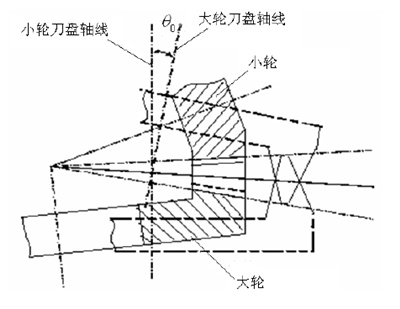
圖 2.6 齒輪齧合時（shí）刀盤的相對位置（zhì）
2.2.2 局部共軛原理
根據成形（xíng）法或展成法加工完成的大輪齒麵，結（jié）合齒輪齧合原理，求出（chū）與大輪共軛的相應小輪的齒麵。求出的小輪齒麵不能在銑齒機上完（wán）成加（jiā）工，為了得到一個與理想齒麵相切並且可以被銑（xǐ）齒機加工出來的實際齒麵，需要將小輪齒麵上選擇的某（mǒu）點 M 四（sì）周的齒麵刮去一（yī）層，如圖 2.7 所示，完成對理論齒麵的修正。這樣處理之後，與大輪齒麵相齧（niè）合的實際（jì）接觸區就會是（shì）一個以 M 點為中心（xīn）的局部接觸區，這（zhè）就是齒輪齧合的局部共軛原理[30]。
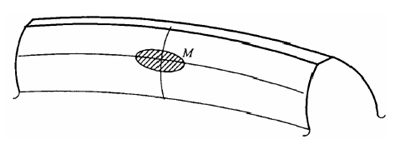
圖（tú） 2.7 局部接（jiē）觸（chù）區示意圖
完全共軛的齒輪副具有承載能力大、噪（zào）聲低、運動平穩等優點，但是該型齒（chǐ）輪副也存在可調性差的缺點，對相關零件製造、安裝誤差的要求較高，如果製造安（ān）裝的過程（chéng）中出現的誤差較（jiào）大，輪齒邊緣就會在齧合傳（chuán）動過程中（zhōng）出現載荷集中而使破壞的問題。局部共軛的（de）齒輪副能夠克服該缺點，即使（shǐ）在安裝位置存在誤差的（de）情況下，也能夠保證接觸區隻能在中點附近移動，避免載荷在輪齒邊緣集中[37]
。基於局部共軛齒輪副在實際生成應用中的優良性能（néng），準雙曲麵齒（chǐ）輪以及其他可以用直（zhí）接（jiē）、間接展成法（fǎ）加（jiā）工的齒輪副（fù），越來越多地（dì）開始采用該方法加工。
2.3 弧（hú）齒錐齒（chǐ）輪齒麵建模
2.3.1 坐標係及參數
（1）工件位置基本參數
1）垂直輪位E02垂直輪位是指被切（qiē）齒輪的中心線與搖台中心線的相對垂（chuí）直偏置量。
2）床位BX2 工件箱沿搖台（tái）中心線方向相對於標準位置前進或後退的距離（lí）即為（wéi）床位。它對被切（qiē）齒輪的切齒深（shēn）度（dù）具有直接影響。
3）軸向輪位修正（zhèng）值X2 工（gōng）件箱（xiāng）在轉（zhuǎn）動底座（zuò）的水平軌道上移（yí）動的距離就是軸向（xiàng）輪（lún）位修正值X2，它（tā）用（yòng）來調整齒輪在機床上的軸向位（wèi）置。
（2）刀具位置基本參數（shù）
1）徑向刀位S2
刀盤中心02O 到大輪加工坐標係原點 O 的距離即為徑向刀位S2。
2）參考（kǎo）點 M 的相位角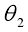
參考點（diǎn） M 點相位角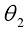
是用來表示參考點（diǎn）在坐（zuò）標（biāo）係中角相（xiàng）位置的參數（shù）。該參數可以完（wán）成刀盤在齒長方向的切（qiē）削加工運動的控製（zhì）。
是用來表示參考點（diǎn）在坐（zuò）標（biāo）係中角相（xiàng）位置的參數（shù）。該參數可以完（wán）成刀盤在齒長方向的切（qiē）削加工運動的控製（zhì）。 3）角向刀位q2 刀盤中心O02和大輪加工坐標係原點 O 的連線與 i 軸（zhóu）的夾角即（jí）為角向刀位q2 。刀盤在齒高方向的切削加工運動就是由該參數控製完成的。除了工件位（wèi）置參數以及刀具位置參數（shù）之外，還有大輪與產形輪的傳動比（bǐ），即滾比02i參數，這也是弧齒錐齒輪齒麵模型建立的重要參數（shù）。
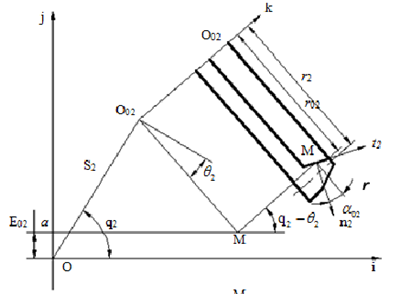
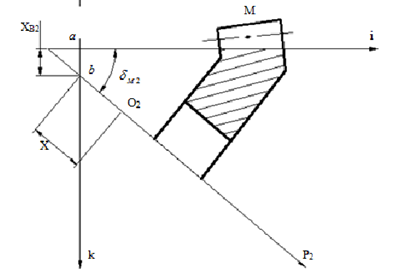
圖2.8 大輪加工坐標係
2.3.2 弧齒錐齒輪齒麵方程
以螺旋（xuán）錐齒輪右旋（xuán）大輪為（wéi）例，論述（shù）齒麵方程的建立過程。圖 2.9 為展成法加工螺旋錐齒輪大輪時所用的雙麵刀盤的軸截麵，圖中a1為雙刀麵內（nèi）刀麵齒形角，a1 為雙刀麵（miàn）外刀麵齒形角，r0為大輪刀盤的名義半徑，W2為刀刃的刀頂距。通過式子（2.22）推算加工大輪凸麵的內刀和加工大輪凹麵的外刀的刀尖直徑[14]。
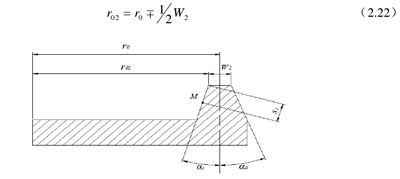
圖 2.9大輪加工用雙麵刀盤
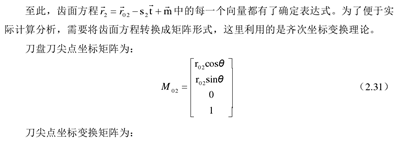
大輪齒麵與刀盤切削麵是（shì）共（gòng）軛（è）的，可以（yǐ）通過共軛曲麵的方（fāng）法求得大輪的齒麵方程。
假設（shè）切削麵為第一曲麵，大輪為第二曲麵，采用第二（èr）共軛曲（qǔ）麵的求解方法建立大輪的齒麵方程。
2.4 本章（zhāng）小結
本章主要對螺旋錐齒輪加工理論的相關知（zhī）識進行了介紹。闡述了齧（niè）合原（yuán）理，分析了能夠解決齒麵幾何問題和運動問（wèn）題的相對微分法，通過齧合方程的（de）建立得（dé）出（chū）運動曲麵持續齧合的（de）前提條件是兩曲麵在法線方向的分速（sù）度必須相等。對弧齒錐齒輪的加工原（yuán）理和方（fāng）法進行了研究，分析（xī）了齒輪齧合的局部共軛原理以及弧齒錐齒輪齒麵建模的過程。相關齧合理論是數（shù）控係統後台（tái）計算處理工作（zuò）的主要依據，為後續（xù）章節人機界麵的開發設計提供了理論支撐。
投稿（gǎo）箱：
如果您有機床行業、企（qǐ）業（yè）相（xiàng）關新聞稿件發表，或進行資訊合作，歡迎聯（lián）係本網編輯部， 郵箱：skjcsc@vip.sina.com
如果您有機床行業、企（qǐ）業（yè）相（xiàng）關新聞稿件發表，或進行資訊合作，歡迎聯（lián）係本網編輯部， 郵箱：skjcsc@vip.sina.com
更多本專題新聞
名企推（tuī）薦（jiàn）
專題點擊前十
| 更多
